Relativistic Kinetic Energy
Introduction
The work-energy theorem is a simple expression that relates the work done on a rigid body (W) to the change in kinetic energy of the body (\(\Delta K\)):
\[\begin{equation} \Delta K = W \end{equation}\]Work is defined as the path integral of force. Writing out this path integral, we arrive at an expression that should be familiar to many students in physics.
\[\begin{equation} \Delta K = W = \int_{x_i}^{x_f} \vec{F} \cdot d\vec{x} \end{equation}\]In the expression above, \(x_i\) and \(x_f\) are the initial and final positions of the rigid body. Although this expression is widely used in classical mechanics, we often forget that the work-energy theorem can be used in special relativity as well. With a bit of simple calculus, it is easy to solve for the kinetic energy of a relativistic particle using the formula above.
Relativistic Work Energy Theorem
Any work done on a point particle will change its kinetic energy - it does not matter if we are analyzing a relativistic or non-relativistic case. The only thing that changes in our analysis of kinetic energy in each case is the expression for force (\(\vec{F}\)). In the non-relativistic situation, we are familiar with Newton’s second law:
\[\begin{equation} \vec{F} = m\vec{a} \end{equation}\]Recall that this is a simplification of the impulse momentum theorem when mass is constant:
\[\begin{equation} \vec{F} = \frac{d\vec{p}}{dt} = \frac{d}{dt} \left [ m\vec{v} \right ] = \vec{v} \frac{dm}{dt} + m\frac{d\vec{v}}{dt} = m\frac{d\vec{v}}{dt} = m\vec{a} \end{equation}\]The impulse-momentum theorem can be used in the relativistic case as well. The only difference is that we will use the relativistic expression for momentum instead of the non-relativistic expression.
\[\begin{equation} \gamma = \frac{1}{\sqrt{1-(v/c)^2}} \end{equation}\] \[\begin{equation} \vec{p} = \gamma m \vec{v} \end{equation}\] \[\begin{equation} \vec{F} = \frac{d\vec{p}}{dt} = \frac{d}{dt} \left [ \gamma m \vec{v} \right ] \end{equation}\]In the expressions above, \(\gamma\) is the Lorentz factor and \(m\) is the rest mass of the particle. The velocity \(\vec{v} = \beta c\) where \(c\) is the speed of light in a vacuum and \(\beta\) is the relativistic beta of the particle. We can solve for the kinetic energy of the particle in a number of ways. I am going to integrate with respect to velocity.
The Derivation
We will orient our axes so that the velocity and force are along the x-axis. Letting \(v_x \equiv v\) and \(F_x \equiv F\) yields:
\[\begin{equation} F = \frac{dp}{dt} = \frac{d}{dt} \left [ \gamma mv \right ] \end{equation}\]Let’s plug this expression for force into the work-energy theorem and change our variable of integration to v. Since momentum and \(\gamma\) are both functions of speed, this substitution will simplify the analysis.
\[\begin{align} \Delta K &= \int_{x_i}^{x_f} \vec{F} \cdot d\vec{x}\\[0.1cm] &= \int_{x_i}^{x_f} F dx cos(0)\\[0.1cm] &= \int_{x_i}^{x_f} F dx\\[0.1cm] &= \int_{x_i}^{x_f} \frac{d}{dt} \left [ \gamma mv \right ] dx\\[0.1cm] &= \int_{t_i}^{t_f} \frac{d}{dt} \left [ \gamma mv \right ] v dt \end{align}\]Now that everything is in terms of speed \(v\) and time \(t\) we can solve this integral by using integration by parts. Just to keep the notation clear, I will use a and b instead of u and v in my expressions. Let:
\[\begin{equation} a = v \Rightarrow da = \frac{dv}{dt} dt \end{equation}\] \[\begin{equation} db = \frac{d}{dt} \left [ \gamma m v \right ] dt \Rightarrow b = \gamma mv \end{equation}\]We then get:
\[\begin{align} \Delta K &= \left [ ab \right ]_{t_i}^{t_f} - \int_{t_i}^{t_f} b da\\[0.1cm] &= \left [ \gamma m v^2 \right ]_{t_i}^{t_f} - \int_{t_i}^{t_f} \gamma mv \frac{dv}{dt} dt\\[0.1cm] &= \left [ \gamma m v^2 \right ]_{v_i}^{v_f} - \int_{v_i}^{v_f} (\gamma mv) dv\\[0.1cm] &= \left [ \frac{m v^2}{\sqrt{1-(v/c)^2}} \right ]_{v_i}^{v_f} - \int_{v_i}^{v_f} \frac{mv}{\sqrt{1-(v/c)^2}} dv \end{align}\]In the last two lines above, we use the fact that the velocity of the system is equal to \(v_i\) at time \(t_i\) and \(v_f\) at time \(t_f\). We can solve the integral above using a simple u-substituion. Let \(u = 1 - (v/c)^2\). Then, \(du = -2v dv/c^2\).
\[\begin{align} \Delta K &= \left [ \frac{m v^2}{\sqrt{1-(v/c)^2}} \right ]_{v_i}^{v_f} - \int_{v_i}^{v_f} \frac{mv}{\sqrt{1-(v/c)^2}} dv\\[0.1cm] &= \left [ \frac{m v_f^2}{\sqrt{1-(v_f/c)^2}} - \frac{m v_i^2}{\sqrt{1-(v_i/c)^2}} \right ] + \frac{mc^2}{2} \int_{1 - (v_i/c)^2}^{1-(v_f/c)^2} \frac{du}{\sqrt{u}}\\[0.1cm] &= \left [ \frac{m v_f^2}{\sqrt{1-(v_f/c)^2}} - \frac{m v_i^2}{\sqrt{1-(v_i/c)^2}} \right ] + \frac{mc^2}{2} \left [ 2\sqrt{u} \right ]_{1 - (v_i/c)^2}^{1-(v_f/c)^2}\\[0.1cm] &= \left [ \frac{m v_f^2}{\sqrt{1-(v_f/c)^2}} - \frac{m v_i^2}{\sqrt{1-(v_i/c)^2}} \right ] + mc^2 \left [ \sqrt{1-(v_f/c)^2} - \sqrt{1-(v_i/c)^2} \right ]\\[0.1cm] &= \left [ \frac{m v_f^2}{\sqrt{1-(v_f/c)^2}} - \frac{m v_i^2}{\sqrt{1-(v_i/c)^2}} \right ] + mc^2 \left [ \frac{1-(v_f/c)^2}{\sqrt{1-(v_f/c)^2}} - \frac{1-(v_i/c)^2}{\sqrt{1-(v_i/c)^2}} \right ]\\[0.1cm] &= \left [ \frac{m v_f^2}{\sqrt{1-(v_f/c)^2}} - \frac{m v_i^2}{\sqrt{1-(v_i/c)^2}} \right ] + \left [ \frac{mc^2}{\sqrt{1-(v_f/c)^2}} - \frac{m v_f^2}{\sqrt{1-(v_f/c)^2}} - \frac{mc^2}{\sqrt{1-(v_i/c)^2}} + \frac{m v_i^2}{\sqrt{1-(v_i/c)^2}} \right ]\\[0.1cm] &= \frac{mc^2}{\sqrt{1-(v_f/c)^2}} - \frac{mc^2}{\sqrt{1-(v_i/c)^2}}\\[0.1cm] &= \gamma_f mc^2 - \gamma_i mc^2\\[0.1cm] &= \left (\gamma_f - \gamma_i \right )mc^2 \end{align}\]Suppose that our particle starts from rest (or we want to use a speed of zero as a baseline). That means \(v_i = 0\) and \(\gamma_i = 1\). Thus, the final expression for the kinetic energy is:
\[\begin{equation} K_f = \left ( \gamma_f - 1 \right ) mc^2 \end{equation}\]I plot the kinetic energy of a particle with mass m = 1 kg at different values of \(\beta\) in the graph below. Note that the kinetic energy of the moving particle is completely determined by its rest mass and the Lorentz factor (along with a couple of constants). As \(\beta \rightarrow 1\) (i.e. the speed of the particle approaches the speed of light) the energy tends to infinity.
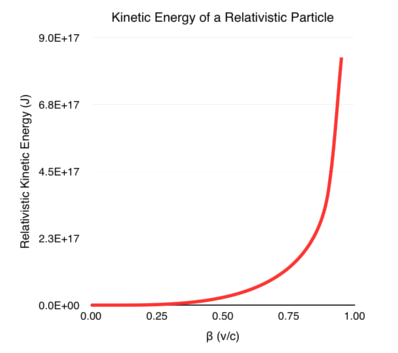
The Low Speed Limit

In a previous blog post I showed how one can expand the Lorentz factor, drop higher order terms, and retrieve the low-speed limit of relativistic expressions. Why don’t we do that here? Recall that the expansion for \(\gamma\) is given by:
\[\begin{equation} \gamma = 1 + \frac{1}{2}\beta^2 + \frac{3}{8}\beta^4 + \frac{5}{16}\beta^6 + \frac{35}{128}\beta^8 + \dots \end{equation}\]Substitute that into our expression for kinetic energy.
\[\begin{equation} K_f = \left ( \frac{1}{2}\beta_f^2 + \frac{3}{8}\beta_f^4 + \frac{5}{16}\beta_f^6 + \frac{35}{128}\beta_f^8 + \dots \right ) mc^2 \end{equation}\]Drop all terms of \(\beta_f^3\) or higher.
\[\begin{equation} K_f \approx \frac{1}{2}\beta^2 mc^2 = \frac{1}{2}mv^2 \end{equation}\]That looks familiar. We got the classical, non-relativistic kinetic energy when we took the low speed limit. Everything is self-consistent! In the figure below, I plot the non-relativistic and relativistic calculations for kinetic energy at different values of \(\beta\). Notice that at low speeds, they match up pretty well. But when \(\beta\) starts to increase, the non-relativistic kinetic energy is way off from the correct relativistic kinetic energy.
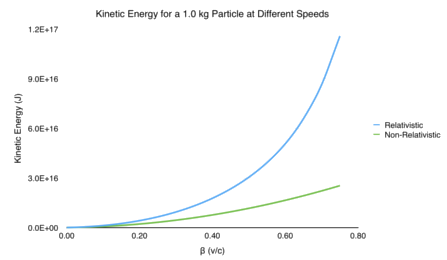
Conclusion
Whenever we break into a new area of physics, we need to remember that our previous knowledge is still valid. Here, we used a simple classical concept to derive the relativistic kinetic energy of a particle.
Until next week!